Kategoria: Bez kategorii

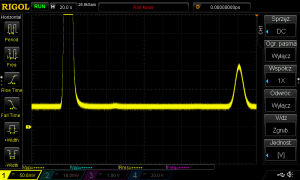
Zarejestrowane impulsy maksymalnie 1,2V.

Dla pamięci:

Jest to wtyczka taka jak ta: https://www.ebay.com/itm/233182744320

Zdemontowana z telewizora znalezionego na śmietniku.

Oznaczenia na etykiecie:

3139 147 17402

UR1316R/AI-3

HJ21 0320 HF32003

Wewnątrz pracuje układ „wszystko w jednym” WINNER1 C250310

Zdemontowany prawdopodobnie z jakiegoś telewizora dla p.cz.

Tak się prezentuje filtr po otwarciu:

Tutaj zdjęcia struktury w powiększeniu:

A tutaj pomiar na analizatorze:

Jak widać, jest to filtr pasmowo-przepustowy o dosyć wysokim tłumieniu i paśmie ok. 33-38,6 MHz. Ciekawe, czy stąd wynika jego nazwa?

Zdjęcia struktury scalonej układu 74LS06 (6 inwerterów z wyjściem typu otwarty kolektor):

Autopsja syrenki alarmowej.

Zasilanie: 12V DC. Syrenka wydaje zmodulowany ton. Goneracją głownego tonu zajmuje się VCO z układu scalonego 4046, a modulacja powstaje na wzmacniaczu operacyjnym LM358 pracującym w roli generatora przebiegu zbliżonego do trójkątnego – zgrubnie scałkowany przebieg prostokątny o niskiej częstotliwości.

Na wyjściu VCO anajduje się tranzystor NPN, który wysterowuje transformator o przekładni ok. 3,66:1. Indukcyjności zwojów to odpowiednio 107mH i 8mH, mierzone dla 1KHz. Transformator podwyższa napięcie, lub jak kto woli dopasowuje impedancję przetwornika piezoakustycznego.

Transformator w syrence zalany jest w obudowie czymś w rodzaju masy epoksydowej, przy wyjmowaniu się uszkodził, ale udało mi się go naprawić, po czym zagrzałem go w rurce termokurczliwej z klejem. Transformator ma 3 wyprowadzenia, jedno z nich (środkowe) jest wspólne dla obu uzwojeń. Z konstrukcyjnego punktu widzenia jest to więc cewka z odczepem.

Z ciekawości podpiąłem sam przetwornik piezoakustyczny pod tester rezonatorów kwarcowych:

Uzyskałem oscylację na częstotliwości dużo wyższej, niż się spodziewałem, bo ok. 112MHz:

Ciekawe.

Testowi zostały poddane:

1. Szybkozłączka rozgałęźna BM 00110
2. Tulejka połączeniowa samolutująca ST-ASS-HST3-1/2
3. Tulejka zaciskowa izolowana BM00162
4. Szybkozłączka Wago 221-412

Złączki obciążyłem prądem 3A z zasilacza warsztatowego (w trybie regulacji prądu). Na przewodzie naciąłem izolację, aby móc dostać się do żyły. Użyty przewód to MXC1000HF 1,00m².

Uzyskane wyniki z pomiaru miliwoltomierzem:

1. 16 mV
2. 6 mV
3. 7 mV
4. 8 mV

Co daje oporności odpowiednio:

1. 5,3 mΩ
2. 2,0 mΩ
3. 2,3 mΩ
4. 2,7 mΩ

Taki żarcik – jak udało Ci się policzyć, podaj wynik.

W zasadzie pierwszy program GUI napisany w Javie. Prymitywny kalkulator.

Pobierz [calc.zip]

Poniższy algorytm oblicza pierwiastek kwadratowy metodą babilońską. Metoda polega na:
1. Zgadnięciu jakiejś liczby, im bliżej prawdziwej wartości pierwiastka, tym lepiej; W poniższym przykładzie brana jest liczba dwukrotnie mniejsza od pierwiastkowanej;
2. Obliczeniu wartości dzielenia pierwiastkowana/”strzał”;
3. Wyznaczeniu średniej arytmetycznej z tych liczb i użycie jej jako kolejnego „strzału”;
4. Powtarzaniu pkt. 2-3; Rozstrzał pomiędzy tymi liczbami z każdą iteracją kurczy się, a średnia przybliża się do realnej wartości pierwiastka.
W poniższym kodzie matlab użytkownik podaje ilość iteracji, jaką ma wykonać program.

% Program obliczajacy wartosc pierwiastka kwadratowego metoda babilonska
% Autor: Aleksander Kaweczynski e.vt0.pl
% 2017-12-17

clc; clear all; close all; format compact;
a=input('Podaj liczbe, z ktorej policzyć pierwiastek: ');
b=a/2; % aktualny 'strzal';
n=input('Podaj ilosc iteracji (liczba calkowita >2)');
c=0; % dzielenie a/strzal
d=0; % srednia z obu
for i=1:n
    c=a/b;
    d=(b+c)/2;
    b=d;
    disp(['Iteracja nr ', int2str(i), ' wynik: ', num2str(b)]);
end

Zamieszczam również wersję w Javascript:

document.getElementById('calculatebabylon').onclick=function(){
	var a = document.getElementById('babylonvalue').value;
    var b=a/2; // aktualny 'strzal';
	var n=10;
	var c=0; // dzielenie a/strzal
	var d=0; // srednia z obu
	document.getElementById('babylonsquare').innerHTML = '';
	for(var i=1;i<=n;++i) {
		c=a/b;
		d=(b+c)/2;
		b=d;
		document.getElementById('babylonsquare').innerHTML += 'Iteracja nr '+ i + ' wynik: ' + b +'<br />';
	}
	document.getElementById('babylonsquare').innerHTML += 'Faktyczna wartosc: ' + Math.sqrt(a);
};